Razonamiento Numérico
Problemas con Regla de Tres Simple
Una de las aplicaciones de proporcionalidad más antigua es la Regla de Tres que resulta al comparar dos o más magnitudes.
REGLA DE TRES SIMPLE DIRECTA
Cuando las magnitudes comparadas son directamente proporcionales.Esquema:1era. magnitud 2da. magnitud
a b
x c
Si son magnitudes directamente proporcionales se cumple :
a/b = x/c
bx = ac

REGLA DE TRES SIMPLE INVERSA
Cuando las magnitudes comparadas son inversamente proporcionales :Esquema:
1era. magnitud 2da. magnitud
a b
x c
Si son magnitudes directamente proporcionales se cumple :
a·b = x·c

PROBLEMAS RESUELTOS DE REGLA DE TRES SIMPLE
Problema #1
Isabel escribe 3/5 de su reporte en 3.2 horas. A la misma velocidad de escritura. ¿Cuántos minutos más necesitará para terminar su reporte?
A) 2 B) 76 C) 85 D) 128 E) 190
Problema #2
Sabiendo que de 250 quintales de remolacha pueden extraerse 30 quintales de azúcar, ¿cuántos quintales de azúcar podrán proporcionar 100 quintales de remolacha?
A) 3 B) 4 C) 6 D) 12 E) 18
Solución:
Notamos que a menos remolacha se obtendrá menors azúcar, por lo tanto son magnitudes directamente proporcionales (D.P.)
=> Remolacha Azúcar
=> 250 30
=> 100 x
Resolviendo
=> x = 100·300/250
=> x = 12 quintales
Respuesta: Proporcionarán 12 quintales de azucar.
Pregunta #3
Para la preparación de una mermelada se necesitan 12 manzanas que cuestan en total $1.60. ¿Cuánto costarán 72 manzanas?
A) $9.0 B) $9.4 C) $9.6 D) $9.8
Problema #4
¿Qué porcentaje es 0,002 de 0,04?
A) 0,05% B) 0,5% C) 0,8% D) 5% E) 8%
Problema #5
Un grupo de 24 excursionistas lleva víveres para 18 días, pero al iniciar la excursión se suman 3 personas más. ¿Cuántos días antes se acabarán los víveres?
A) 2 B) 4 C) 6 D) 8 E) 16
Solución:
Se puede notar que a más personas los víveres durarán menos días, por lo tanto se trata de magnitudes inversamente proporcionales.
#Excursionistas #Días
24 18
27 x
Despejando x
x = 24·18/27
x = 16 días
Respuesta: Se acabarán en 18-16 = 2 días antes.
Pregunta #6
Si 1 Kg de naranjas contiene de 6 a 8 manzanas. ¿Cuál es el mayor peso que pueden tener cuatro docenas de naranajas?
A) 48 Kg B) 6 Kg C) 10 Kg D) 12 Kg E) 8 Kg
Pregunta #7
Ocho hombres han cavado en 20 días una zanja de 50m de largo, 4m de ancho y 2m de profundidad. ¿En cuánto tiempo hubieran cavado la zanja 6 hombres menos?
Solución:
Como la obra es la misma, planteamos la siguiente regla de tres:
Número de hombres tiempo
8 20
2 t
Se trata de una regla de tres simple inversa porque a más hombres menos tiempo para realizar la obra, entonces
=> t/20 = 8/2
=> t = 20·4
=> t = 80
Respuesta: Con 6 hombres menos se necesitan 80 días para terminar la obra.
Problema #8
Un labrador tiene forraje para alimentar a una vaca durante 18 días y si fuera una oveja tendría para 36 días. ¿Para cuánto tiempo tendría forraje si tuviera 2 vacas y una oveja?
A) 18 días B) 12,5 días C) 9,4 días D) 7,2 días E) 5 días
Problema #9
Un barco tiene provisiones para 24 días y las distribuye equitativamente a todos los tripulantes. Si se desea que las provisiones duren 6 días más, ¿en que fracción se debe reducir la ración de cada tripulante?
A) 1/2 B) 1/4 C) 1/5 D) 1/6 E) 1/8
Solución:
Podemos observar que las magnitudes que intervienen son número de días y ración. Si queremos que las provisiones duren más días, entonces se debe disminuir la ración en cada tripulante; por lo tanto son inversamente proporcionales. Consideramos que la ración inicial es la unidad y "x" la fracción que se debe disminuir, luego se hará el siguiente planteamiento.
#de días ración
24 1
30 1-x
Resolviendo
30(1- x) = 24·1
30 - 30x = 24
x = 1/5
Respuesta: Por tanto, a cada tripulante se le debe reducir en un 1/5 de su ración.
Pregunta #10
Mateo es el triple de rápido que Omar al realizar una tarea. Si juntos pueden culminar la tarea en 15 días, ¿cuántos días emplearía Mateo para realizar la misma tarea trabajando solo?
A) 16 B) 18 C) 20 D) 22 E) 24
Problema #11
Según las ordenanzas municipales de cierta ciudad lo máximo que puede construirse en determinada zona corresponde a 20 pisos de 3 m de altura cada uno. ¿Qué altura deberá tener cada piso si en dicha zona se desea construir un edificio de 30 plantas?
A) 1 m B) 1,5 m C) 2 m D) 2.5 m E) 3 m
Solución:
Las magnitudes que comparamos son el número de pisos y la altura de cada piso. Como la altura de los 20 pisos es la máxima, entonces estas magnitudes se deben relacionar de manera inversa.
#pisos altura (m)
20 3
30 x
Resolviendo
=> x/3 = 20/30
=> x = 2
Respuesta: Cada piso debe tener una altura de 2 m.
Pregunta #12
Si un campanario toca 10 campanadas en 27 segundos. ¿Cuántas campanadas tocará en un minuto?
A) 20 B) 18 C) 22 D) 21 E) N.A.
Problema #13
Para pavimentar un gran hipermercado se han empleado 10 000 baldosas cada una de las cuales mide 800 cm2 de superficie. ¿Cuántas baldosas se habrían utilizado si el tamaño de cada una fuera de sólo 100 cm2?
A) 12 000 B) 15 000 C) 18 000 D) 20 000 E) 24 000
Solución:
Notemos que si las baldosas son más pequeñas se necesitaran una mayor cantidad de ellas para pavimentar la misma área del hipermercado, por tanto las magnitudes tienen un relación inversa.
#baldosas área por baldosa (cm2)
10 000 800
x 100
Despejamos x
=> x/10000 = 800/100
=> x = 18 000
Respuesta: Se necesitan 18 000 baldosas.
Pregunta #14
Mateo es el triple de rápido que Omar al realizar una tarea. Si juntos pueden culminar la tarea en 15 días, ¿cuántos días emplearía Mateo para realizar la misma tarea trabajando solo?
A) 16 B) 18 C) 20 D) 22 E) 24
Pregunta #15
Un sastre pensó hacer un terno en una semana; pero tardó 4 días más por trabajar 4 horas menos cada día. ¿Cuántas horas trabajó diariamente?
A) 11 B) 7 C) 8 D) 14 E) 22
Solución:
Suponemos que el sastre inicialmente trabajó x horas por día, entonces con los datos del problema planteamos la siguiente regla de tres simple:
Número de horas Número de días
x 7
x - 4 11
Como a más horas de trabajo por día menos tiempo se demora en hacer el traje, entonces se trata de una regla de tres simple inversa, resolviendo:
=> x/(x - 4) = 11/7
=> 7x = 11(x-4)
=> 7x = 11x - 44
=> -4x = -44
=> x = 11
Respuesta: El sastre trabajó diariamente 11 horas.
Pregunta #16
Un campanario emplea 6 segundos para tocar 4 campanadas. ¿Cuánto tiempo empleará para tocar 8 campanadas?
A) 12 s B) 14 s C) 20 s D) 16 s E) N.A.
Pregunta #17
Un burro atado a una cuerda de 3 metros de longitud tarda 5 días en comer todo el pasto que está a su alcance. Cierto día, su dueño lo amarra a una cuerda más grande y se demora 20 días en comer el pasto que está a su alcance. Hallar la longitud de la nueva cuerda.
A) 4 m B) 5 m C) 6 m D) 12 m E) 18 m
Solución:
El burrro al estar atado a una cuerda tiene un alcance circular para comer todo el pasto a su alrededor, teniendo en cuenta esto planteamos la siguiente regla de tres simple:
Area(m2) Número de días
π·32 5
π·x2 20
Como a más cuerda se tiene un mayor alcance (mayor área del círculo) y por tanto el burro se demora más tiempo en comer, entonces se trata de una regla de tres simple, resolviendo:
=> π·x2/ π·32 = 20/5
=> x2/ 32 = 4
=> x2 = 4·9
=> x = 6 m
Respuesta: La longuitud de la nueva cuerda es de 6 metros.
Pregunta #18
¿Qué porcentaje es 60 de 1/2?
A) 25% B) 12000% C) 1000% D) 24000%
Pregunta #19
Si 20 litros de agua contienen 15% de sal, ¿Qué cantidad de agua se debe evaporar para que la nueva solución contenga 20% de sal?
A) 6L B) 4L C) 5L D) 3L
Pregunta #20
Un grifo atascado gotea 0,042 litros cada minuto. ¿Cuántos litros de agua se perderán en un día?
A) 60,48 B) 1,008 C) 42,00 D) 151,20
Pregunta #21
Un grupo de marineros tienen alimentos para 15 días; pero si hubiese 2 marinos más, los alimentos durarían 3 días menos. ¿Cuántos marineros integran el grupo?
A) 6 B) 8 C) 12 D) 18
Pregunta #22
Veinticinco panes cuestan tantos dólares como panes se pueden comprar con un dólar. ¿Cuántos céntimos cuestan cada pan?
A) 5 B) 10 C) 20 D) 25
Pregunta #23
Juan es el doble de rápido que Pedro. Si juntos pueden hacer una obra en 10 días, cuánto tiempo le tomará a Juan hacerlo solo?
A) 13 días B) 14 días C) 15 días D) 16 días
Preguntas propuestas de Regla de Tres Simple

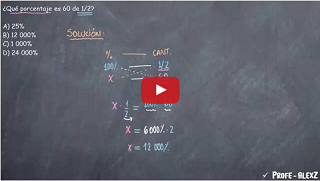






No hay comentarios.:
Publicar un comentario