
RAZONAMIENTO NUMERICO
Problemas con Planteo de Ecuaciones.
El plantear una ecuación significa que el enunciado de cualquier problema que se tenga hay que interpretarlo, entenderlo y una vez comprendido, hay que expresarlo en una ecuación matemática, lo cual dará solución al problema planteado.
Problema 1
La edad de Cristina es un tercio de la de su padre y dentro de 16 años será la mitad, entonces la edad de Cristina es:
A) 16 años B) 24 años C) 36 años D) 48 años
Problema 2
La suma de dos números es 24. Tres veces el mayor excede en dos unidades a cuatro veces el menor. Hallar los números.
A) 14 y 16 B) 8 y 14 C) 20 y 10 D) 14 y 10
Problema 3
La suma de A más B es 116. A es 3 menos que C y al mismo tiempo A es 4 más que B. ¿Qué número es C?
A) 63 B) 58 C) 65 D) 67
Problema 4
Si 80 excede a 60 en 2x, hallar “x”:
A) 8 B) 5 C) 10 D) 4 E) 6
Solución:
Nos dice que 80 excede, significa que es mayor, ¿y a quien excede?, nos dice a 60, ¿y en cuanto?, nos dice en 2x , identificamos y planteamos:
Cantidad mayor = 80, Cantidad menor = 60, Exceso = 2x
=> 80-60 = 2x
=> 20 = 2x
=> x = 10
Respuesta: 10.
Problema 5
Dos veces el área de un cuadrado de lado L es igual a cuatro veces el área de un triángulo de altura L. ¿Cuál es la base del triángulo?
A) 2L B) L C) 1/2L D) 2L/2
Problema 6
Un número excede a 10 tanto como es excedido por 40. ¿hallar el número?
A) 18 B) 25 C) 10 D) 44 E) 26
Solución:
Nos indica que el numero desconocido excede a 10, osea el numero es mayor que 10 tanto (en la misma cantidad o igual), como la cantidad es menor que 40.
Sea “x” la cantidad desconocida, entonces:
=> Un numero excede a 10: x-10,
=> Es excedido por 40: 40-x
Planteamos la ecuación:
=> x-10 = 40-x
=> 2x = 40 + 10
=> 2x = 50
=> x = 25
Respuesta: Por lo tanto: dicho numero es “25”.
Problema 7
Si x/y = -1, entonces x+y =?
A) 1 B) 2x C) 2y D) 0
Problema 8
El exceso del triple de un numero sobre 42 equivale al exceso de 226 sobre el numero. ¿Cuál es el número?
A) 82 B) 65 C) 40 D) 67 E) 16
Solución:
Seal x el numero desconocido.
El exceso del triple de un numero sobre 42: 3x - 42
El xceso de 226 sobre el numero: 226 – x
Entonces podemos plantear:
=> 3x – 42 = 226 – x
=> 4x = 268
=> x = 67
Respuesta: 67.
Problema 9
¿Cuál es el valor de m si: (1 + 3m)/3 = 2m ?
A) 1/3 B) 1 C) -1/3 D) -1 E) -2
Problema 10
¿Cuál es el número cuyo 2/5 equivale a 50?
A) 83 B) 135 C) 120 D) 125
Problema 11
Juan tiene los 5/6 de lo que tiene Pedro. Si Juan recibe $80 de Pedro, éste tiene los 2/5 de lo de Juan. ¿Cuánto tiene Pedro?
A) $100 B) $138 C) $168 D) $200
Problema 12
Hallar dos números sabiendo que uno excede al otro en 8 unidades y que el menor es 35
unidades menos que el doble del mayor
A)18 y 10 B)15 y 20 C) 32 y 12 D) 24 y 27 E) 19 y 27
Solución:
Como nos dicen que uno de los números excede al otro en 8, entonces sean los números:
- numero menor: x
- numero mayor: x + 8
Según el enunciado:
=> x = 2(x + 8) – 35
=> x = 2x + 16 –35
=> x = 19
Respuesta: Numero menor 19 y numero mayor 27.
Problema 13
En un examen aprobaron 2/3 de los niños y 3/4 de las niñas; además el examen lo aprobaron el mismo numero de niños que de niñas. El mínimo numero posible de estudiantes en la clase es:
A) 17 B) 24 C) 27 D) 14
Problema 14
Caperucita Roja va por el bosque llevando una cesta de manzanas rojas para su abuelita. Si en el camino la detiene el lobo y le pregunta ¿cuántas manzanas llevas en tu canasta? Caperucita para confundirlo y escapar le dice: "llevo tantas decenas como el número de docenas más uno". ¿Cuántas manzanas lleva Caperucita Roja?
A) 30 B) 6 C) 60 D) 120 E) 180
Solución:
Sea "x" el número de manzanas, entonces:
Número de decenas = x/10
Número de docenas = x/12
Del enunciado del problema:
=> x/10 = x/12 + 1
Multiplicamos por 60
=> 6x = 5x + 60
=> x = 60
Respuesta: Caperucita Roja lleva 60 manzanas.
Problema 15
Un aeroplano recorrió 1940 km el primer día, el segundo recorrió 340 km más que el primero y el tercero 890 km menos que entre los dos anteriores. ¿Cuántos km recorrió el aeroplano en total?
A) 345 km B) 6678 km C) 7550 km D) 2341 km
Problema 16
Si subo una escalera de 4 en 4 escalones, doy 4 pasos más que subiendo de 5 en 5 escalones. ¿Cuántos escalones tiene la escalera?
A) 50 B) 60 C)70 D) 80 E) 90
Solución:
La cantidad de pasos se halla dividiendo el número de escalones entre número de escalones que se da en 1 paso:
=> #pasos = (#escalones)/(#escalones_en_un_paso)
Sea x el número de escalones en total, entonces
=> #de pasos(4 en 4) = x/4
=> #de pasos(5 en 5) = x/5
Según el problema:
=> x/4 - x/5 = 4
=> x/20 = 4
=> x = 80
Respuesta: La escalera tiene 80 escalones.
Problema 17
Sabiendo que 3 números enteros consecutivos suman 204, calcula la suma de las cifras del número intermedio.
| A) 10 | B) 12 | C) 13 | D) 14 |
Problema 18
María compra treinta metros de tela por cierta cantidad de dinero. Si cada metro de tela hubiera costado S/. 10 menos, hubiese podido comprar 10 metros más con la misma cantidad de dinero. Halle la suma de cifras del precio en soles de un metro de tela.
A)1 B) 2 C) 3 D) 4 E) 5
Solución:
Cantidad de metros de tela: 30m
Precio total: x
Precio por metro de tela: x/30
Del enunciado del problema
=> (x/30 - 10)·(30 + 10) = x
=> 40/30x - 400 = x
=> 40/30x - x = 400
=> 10/30x = 400
=> x = 1200
El precio por metro de tela: 1200/30 = 40
Respuesta: La suma de cifras del precio de un metro de tela es: 4+0 = 4.
Problema 19
De mi dinero 2/3 es equivalente a $50. Gasto 11/15 de mi dinero. ¿Cuánto dinero me queda?
A) $10 B) $20 C) $75 D) $55
Problema 20
En una reunión se encuentran tantos hombres, como tres veces el número de mujeres. Después se retiran 8 parejas; y el número de hombres que aún quedan es igual a 4 veces más, que el número de mujeres que quedan. ¿Cuántas personas en total había al inicio de la reunión?
A) 64 B) 16 C) 48 D) 58 E) 72
Solución:
Número de mujeres: x
Número de hombres: 3x
Si se retiran 8 parejas, entonces
Número de mujeres: x-8
Número de hombres: 3x-8
Del enunciado del problema
=> 3x-8 = 4(x-8)
=> 3x -8 = 4x - 32 + x - 8
=> 2x = 32
=> x = 16
Hallamos la cantidad de hombres y mujeres:
Número de mujeres: x = 16
Número de hombres: 3x = 3(16) = 48
Respuesta: Las personas que habían al inicio de la reunión son: 48+16 = 64.
Problema 21
La suma de las edades de tres hijos es igual a la edad de su madre. Si la madre tiene 48 años, y cada uno de los hijos tiene 2 años más que el anterior, ¿cuáles son sus edades?
| A) 10; 12; 14 | B) 12; 14; 16 | C) 14; 16; 18 | D) 16; 18; 20 |
Problema 22
Marilyn dice : "Dentro de 16 años mi edad será 4 veces la edad que tenía hace 14 años"
¿Qué edad tengo en años?
a) 26 b) 20 c) 18 d) 29 e) 24
Solución:
Edad actual: x
Edad hace 14 años: x - 14
Edad dentro de 16 años: x + 16
Del enunciado del problema:
x + 16 = 4(x - 14)
x + 16 = 4x - 56
3x = 72
x = 24
Respuesta: La edad de Marilyn es 24 años.
Problema 23
Dos de cinco hermanos están conversando:
- Jaime dice: “Tengo 9 años y soy el menor de todos”.
- Rafael dice: “Cada uno de nosotros es mayor en 2 años que el menor inmediato”.
Da como respuesta la suma de las edades de los cinco hermanos.
A) 65 años B) 64 años C) 66 años D) 62 años
Problema 24
Hace 6 años tenía la mitad de los años que tendré dentro de 4 años. ¿Cuántos años tendré dentro de 10 años?
a) 28 b) 29 c) 32 d) 26 e) 18
Solución:
Mi edad actual: x
Mi edad hace 6 años: x - 6
Mi edad dentro de 4 años: x + 4
Del enunciado del problema:
x - 6 = 1/2(x + 4)
2x - 12 = x + 4
x = 16
Respuesta: Dentro de 10 años tendré 16 + 10 = 26 años.
Problema 25
Luis dice: “Si al doble de mi edad se le quita 10 años, se obtendrá lo que me falta para tener 26 años”. Indique cuántos años le faltan a Luis para cumplir el doble de la edad que tenía hace 5 años.
A) 1 B) 2 C) 5 D) 7 E) 12
Problema 26
La edad de Liliana es a la edad de Emilio como 4 es a 7. Dentro de 10 años Liliana tendrá el doble de la edad que tenía Emilio hace 5 años. ¿Cuántos años tiene Emilio?.
a) 12 años b) 14 años c) 9 años d) 10 años e) 21 años
Solución:
"La edad de Liliana es a la edad de Emilio como 4 es a 7"
Edad de Liliana: 4k
Edad de Emilio: 7k
"Dentro de 10 años Liliana tendrá el doble de la edad que tenía Emilio hace 5 años"
Edad de Liliana dentro de 10 años: 4k + 10
Edad de Emilio hace 5 años: 7k - 5
Del enunciado del problema:
4k + 10 = 2(7k - 5)
4k + 10 = 14k - 10
10k = 20
k = 2
"¿Cuántos años tiene Emilio?"
Respuesta: Edad de Emilio: 7k = 7(2) = 14 años
Problema 27
¿Qué hora es cuando la parte transcurrida del día es igual a los 7/5 de lo que falta para acabarse el día?
A) 15:00 B) 12:00 C) 10:00 D) 14:00
Problema 28
Jorge le dice Jhony: "Hace 10 años mi edad excedía al doble de la tuya en 5 años. Si dentro de 15 años mi edad será a la tuya como 3 es a 2, ¿qué edad tenías hace 5 años?"
A) 10 años B) 15 años C) 20 años D) 25 años E) 30 años
Solución:
Sea la edad actual de Jorge y Jhony: x, y
Edad hace 10 años de Jorge: x-10
Edad hace 10 años de Jhony: y-10
Deacuerdo al problema
=> x-10 = 2(y-10) + 5
Dentro de 15 años
=> (x+15)/(y+15) = 3/2
Resolviendo las ecuaciones tenemos que
=> x = 45, y = 25
Respuesta: La edad de Jhony hace 5 años fue 25-5 = 20 años.
Problema 29
La edad que tendré dentro de 20 años será 2 veces más que la edad que tuve hace 10 años ¿Qué edad tendré dentro de 5 años.
A) 20 B) 25 C) 30 D) 35

Problema 30
Araceli tiene 2 cajas de chocolates, una contiene 36 unidades de 10g cada una y la otra 24 unidades de 25g cada una. ¿Cuántos chocolates debe intercambiar Araceli, de modo que ambas cajas mantengan sus cantidades iniciales y el peso de los chocolates de ambas cajas sea el mismo?
A) 6 B) 12 C) 10 D) 8 E) 16
Solución:
Cantidad de chocolates que intercambia de una caja a otra: x
Peso de la primera caja : 36·10 = 360g
Peso de la segunda caja: 24·25 = 600g
Despues de hacer el intercambio, el peso de las cajas debe ser el mismo
=> 360-10x + 25x = 600-25x + 10x
Resolviendo la ecuación tenemos que
=> x = 8
Respuesta: Araceli debe intercambiar ocho chocolates.
Preguntas resueltas de Planteo de Ecuaciones Literales
Una ecuación literal es aquella en la que una o más de las cantidades conocidas se representan mediante el uso de letras en lugar de números.
Ejemplo: a + bx = dy + c
Por lo general, las cantidades conocidas se representan con las primeras letras del alfabeto a, b, c... y las incógnitas con las letras finales x, y, z. Este tipo de ecuaciones, lo podemos encontrar en fórmulas de geométria perímetros, áreas, volúmenes, etc. donde se hace uso de literales.
Pregunta 1
En un examen, un alumno gana “a” puntos por cada respuesta correcta y pierde “b” puntos por cada respuesta equivocada. Después de haber contestado “n” preguntas, obtiene “c” puntos. ¿Cuántas preguntas respondió correctamente?
A) (an+c)/(a-b) B) (bn+c)/(a+b) C) (bn+c)/(a-c)
D) (an+c)/(a+b) E) (bn+c)/(a+b)
Pregunta 2
"La edad de un padre es el cuádruple de la de su hijo y dentro de cinco años será el triple". Si x es la edad del padre, la ecuación correspondiente es:
A) 4(x+5) = 3(x+5) B) 4x + 5 = 3x + 5
C) 4x + 5 = 3 (x+5) D) 4(x+5) = 3(x+20)
E) 3(4x + 5) = 3x
Pregunta 3
El enunciado: “el cuadrado de la suma de dos números x y y es igual al doble de la diferencia de los cuadrados de esos números”, se expresa:
A) x2 + y2 = 2(x – y)2 B) x2 + y2 = 2(x2– y2)
C) (x + y)2 = 2(x – y)2 D) (x + y)2 = 2(x2– y2)
Pregunta 4
Si la edad de una persona en y años más será x años, ¿cuántos años tiene?
A) y B) x + y C) x - y D) x
Pregunta 5
Una joven debe lavar n docenas de camisas; recibirá "a" dólares por cada camisa bien lavada y pagará "b" dólares por cada camisa mal lavada. Si recibió "m" dólares en total, ¿Cuántas camisas fueron mal lavadas?
A) (12an - m)/(a + b) B) (m + 12an)/(a + b) C) (an - m)/(a + b)
D) (m - an)/(12a + b) E) (12am - n)/(a + b)
EJERCICIOS DE ECUACIONES PARA RESOLVER


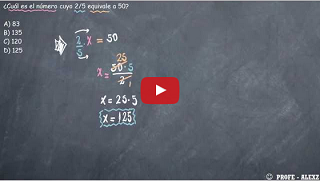










No hay comentarios.:
Publicar un comentario